Tutorial: Simulasi monte carlo untuk prediksi penjualan sepatu

Oleh Prof. Dedi Rosadi, S.Si., M.Sc.

Tim Mahasiswa

1. Arum Shelly Rahma (19/439208/PA/19031)
2. Febina Nur Sabilla Azahra (19/439210/PA/19033)
3. Hidayah Budi Sayekti (19/445717/PA/19541)
4. Julius Satya Ratnandi (19/442595/PA/19344)
5. Khairunnisa Adinda (19/439212/PA/19035)

 

Diketahui sebuah toko sepatu mmengetahui distribusi permintaan sepatu per harinya selama 100 hari terakhir mengikuti pola distribusi sebagai berikut:

No	Permintaan	Frekuensi permintaan
1	4 pasang	5
2	5 pasang	10
3	6 pasang	15
4	7 pasang	30
5	8 pasang	25
6	9 pasang	15
Jumlah		100

 

Lakukan prediksi sepuluh hari kedepan menggunakan pendekatan simulasi monte carlo!

Untuk melakukan simulasi monte carlo untuk kajian prediksi empirik dilakukan dengan algoritma sebagai berikut

1. HItung distribusi frekuensi empirik dan distribusi kumulatif empirik dari data

2. Susun tabel koding sesuai dengan kelas distribusi kumulatif empirik

3. Bangkitkan bilangan random uniform dan cocokkan dengan kelas distribusi kumulatif empirik yang bersesuaian. Nilai ramalan adalah kelas yang diperoleh di langkah ini .

Algoritma ini dapat diaplikasikan sebagai berikut:

Syntax :

#Membuat fungsi bernama simulasi.mc

#dengan parameter x, y, dan n

#x merupakan banyak permintaan

#y merupakan frekuensi

#n merupakan jumlah hari ke depan yang akan diprediksi

simulasi.mc=function(x,y,n){

  #Menentukan nilai pdf

  #yaitu frekuensi dibagi dengan jumlah frekuensi

  pdf=round(y/sum(y),2)

  #Menentukan nilai cdf dengan perulangan

  #awalnya diinisialisasi nilai cdf masih kosong

  cdf=NULL

  #nilai cdf ke 1 sama dengan nilai pdf ke 1

  cdf[1]=pdf[1]

  #melakukan perulangan i dari 2 hingga panjang y

  for(i in 2:length(y)){

  #nilai cdf ke i adalah pdf ke i ditambah dengan cdf ke (i-1)

    cdf[i]=cdf[i–1]+pdf[i]

  }

  #Menyimpan variabel x,y,pdf, dan cdf dalam data frame bernama tabel1

  #nilai x disimpan dalam variabel permintaan

  #nilai y disimpan dalam variabel frekuensi

  tabel1=data.frame(permintaan=x,freq=y,pdf,cdf)

  #Menampilkan tabel1

  print(tabel1)

  #merandom bilangan sebanyak n

  random=runif(n)

  cat(“\n”)

  #Menampilkan bilangan random yang terpilih dalam desimal 2 angka belakang koma

  cat(“Nilai Random: “,round(random,2),”\n”)

  #Menginisialisasi nilai kesimpulan yaitu masih kosong

  kesimpulan=NULL

  cat(“\n”)

  #Membandingkan bilangan random dengan interval bilangan random

  #dilakukan dengan perulangan dari i bernilai 1 hingga n

  for(i in 1:n){

    #jika nilai bilangan random ke i tidak lebih dari cdf[1]

    if(round(random,2)[i]<=cdf[1]){

      #nilai kesimpulan ke i sebesar x[1]

      kesimpulan[i]=x[1]

    }

    #jika nilai bilangan random ke i tidak lebih dari cdf[2]

    else if(round(random,2)[i]<=cdf[2]){

      #nilai kesimpulan ke i sebesar x[2]

      kesimpulan[i]=x[2]

    }

    #jika nilai bilangan random ke i tidak lebih dari cdf[3]

    else if(round(random,2)[i]<=cdf[3]){

      #nilai kesimpulan ke i sebesar x[3]

      kesimpulan[i]=x[3]

    }

    #jika nilai bilangan random ke i tidak lebih dari cdf[4]

    else if(round(random,2)[i]<=cdf[4]){

      #nilai kesimpulan ke i sebesar x[4]

      kesimpulan[i]=x[4]

    }

    #jika nilai bilangan random ke i tidak lebih dari cdf[5]

    else if(round(random,2)[i]<=cdf[5]){

    #nilai kesimpulan ke i sebesar x[5]

      kesimpulan[i]=x[5]

    }

    #jika nilai variabel i tidak dari salah satu nilai di atas

    else {

    #nilai kesimpulan ke i sebesar x[6]

      kesimpulan[i]=x[6]

    }

  }

  #mencetak tabel ramalan banyaknya permintaan

  tabel2=data.frame(Hari=c(1:n),Banyak.Permintaan=kesimpulan)

  print(tabel2)

  #Menentukan jumlah dari kesimpulan dalam variabel total

  total=sum(kesimpulan)

  #Menentukan rata rata dari kesimpulan dalam variabel rata2

  rata2=mean(kesimpulan)

  cat(“Jumlah permintaan sepatu  dalam 10 hari ke depan: “,total,”pasang sepatu”,”\n”)

  cat(“Rata rata permintaan sepatu dalam 1 hari: “,round(rata2,0),”pasang sepatu”,”\n”)

}

#Menetapkan nilai variabel permintaan yaitu berupa vektor

permintaan=c(4,5,6,7,8,9)

#Menentukan nilai variabel frekuensi yang berupa vektor

freq=c(5,10,15,30,25,15)

#Menentukan nilai n sebesar 10 karena ingin diprediksi 10 hari ke depan

n=10

#Memanggil fungsi simulasi.mc

#dengan parameter x adalah permintaan

#parameter y adalah frekuensi

#parameter n adalah n

simulasi.mc(permintaan,freq,10)

 

Output dari Program:

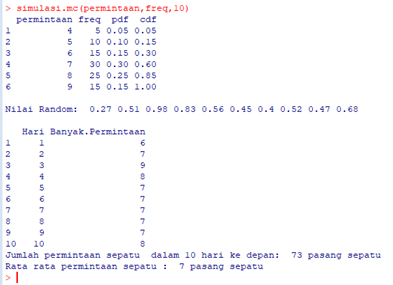
Interpretasi

Dari output simulasi monte carlo di atas kita dapat menentukan banyaknya permintaan sepatu dalam 10 hari ke depan. Sebelumnya telah ditetapkan nilai pdf dan cdf yang akan digunakan. Dengan fungsi simulasi.monte.carlo yag telah ditentukan, kemudian ditetapkan parameter yang akan digunakan. Dalam hal ini digunakan parameter banyaknya permintaan,  frekuensi, dan jumlah hari ke depan yang akan diprediksi. Dari output, didapatkan bilangan random sebagai berikut. Bilangan random ini digunakan untuk menentukan banyaknya permintaam di tiap harinya.

0.27 0.51 0.98 0.83 0.56 0.45 0.4 0.52 0.47 0.68

• Bilangan random pertama yaitu 0.27 masuk dalam interval cdf antara 0.15 dan 0.30, maka banyaknya permintaan sepatu pada hari pertama adalah 6 pasang sepatu.
• Bilangan random kedua yaitu 0.51 masuk dalam interval cdf antara 0.30 dan 0.60, maka banyaknya permintaan sepatu pada hari kedua adalah 7 pasang sepatu.
• Bilangan random ketiga yaitu 0.98 masuk dalam interval cdf antara 0.85 dan 1.00, maka banyaknya permintaan sepatu pada hari ketiga adalah 9 pasang sepatu.
• Bilangan random keempat yaitu 0.83 masuk dalam interval cdf antara 0.60 dan 0.85, maka banyaknya permintaan sepatu pada hari keempat adalah 8 pasang sepatu.
• Bilangan random kelima yaitu 0.56 masuk dalam interval cdf antara 0.30 dan 0.60, maka banyaknya permintaan sepatu pada hari kelima adalah 7 pasang sepatu.
• Bilangan random keenam yaitu 0.45 masuk dalam interval cdf antara 0.30 dan 0.60, maka banyaknya permintaan sepatu pada hari keenam adalah 7 pasang sepatu.
• Bilangan random ketujuh yaitu 0.4 masuk dalam interval cdf antara 0.30 dan 0.60, maka banyaknya permintaan sepatu pada hari ketujuh adalah 7 pasang sepatu.
• Bilangan random kedelapan yaitu 0.52 masuk dalam interval cdf antara 0.30 dan 0.60, maka banyaknya permintaan sepatu pada hari kedelapan adalah 7 pasang sepatu.
• Bilangan random kesembilan yaitu 0.47 masuk dalam interval cdf antara 0.30 dan 0.60, maka banyaknya permintaan sepatu pada hari kesembilan adalah 7 pasang sepatu.
• Bilangan random kesepuluh yaitu 0.68 masuk dalam interval cdf antara 0.60 dan 0.85, maka banyaknya permintaan sepatu pada hari kesepuluh adalah 8 pasang sepatu.

Selanjutnya diperoleh permintaan sepatu dalam 10 hari ke depan sebesar 73 pasang sepatu dan memiki rata rata permintaan sebesar 7 pasang sepatu.