oleh
Prof. Dr.rer.nat. Dedi Rosadi, S.Si., M.Sc.
Tim Mahasiswa
Maria Lidya Natalia M. (19/439213/PA/19036)
Tetuko Titah Gusti (19/439218/PA/19041)
Pingky Oktiawati (19/439215/PA/19038)
Venessa Yumadila Syahra (19/445727/PA/19551)
Vincensius Dimas R (19/445728/PA/19552)
Salah satu teknik untuk pembangkitan bilangan random yang populer adalah pendekatan metode inverse transform. Berikut akan dijelaskan bagaimana melakukan pembangkitan bilangan random berdistribusi uniform(a,b) dan Weibull dengan pendekatan ini, berserta syntax program dengan R untuk pembangkitan data.
Distribusi Uniform
Distribusi uniform dengan parameter nilai batas bawah (a) dan batas atas (b), intervalnya memiliki fungsi distribusi kumulatif sebagai berikut: F(x)=(x-a)/(b-a)
Misalkan U~unif(0,1), maka X =Finv(u) dapat ditransformasikan menjadi: X=u(b-a)+a
Dengan menggunakan R, bilangan random uniform(a,b) dapat dibangkitkan dengan cara sebagai berikut
Syntax
| bangkit.unif<-function(n,a,b){
#membuat fungsi untuk membangkitkan n bilangan random yang berdistribusi uniform dengan parameter n, a, dan b (batas interval) U=runif(n,0,1) #dimisalkan U~unif(0,1) x=U*(b-a)+a #menghitung nilai random yang berdistribusi uniform return(x) #return nilai x sebagai output fungsi bangkit.unif } data1=bangkit.unif(50,3,10) #contoh pemanggilan fungsi bangkit.unif untuk n = 50, a = 3, dan b = 10, lalu disimpan ke variabel data1 data1 #menampilkan hasil pembangkitan distribusi uniform ks.test(data1,”punif”,3,10) #uji Kolmogorov-smirnov untuk mengecek apakah berdistribusi uniform atau tidak |
Output
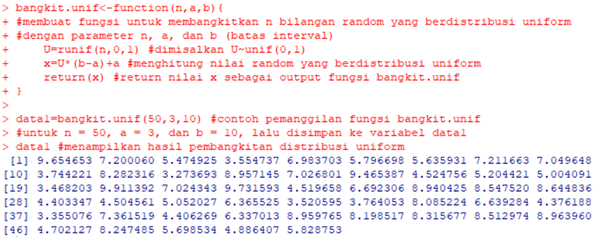

Dengan hipotesis netral data berdistribusi uniform dengan batas bawah = 3 dan batas atas = 10. Diperoleh p-value = 0.9627 > Alpha (0.05), atau dapat disimpulkan bahwa hipotesis netral tidak ditolak atau dalam kata lain sampel random yang dibangkitkan memang benar berdistribusi uniform dengan batas bawah = 3 dan batas atas = 10.
Distribusi Weibull
Diketahui fungsi distribusi kumulatif (CDF) dari distribusi Weibull sebagai berikut
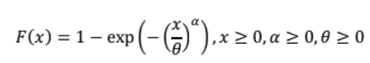
Misalkan ~ Unif(0,1) , maka dapat ditransformasikan sebagai berikut :
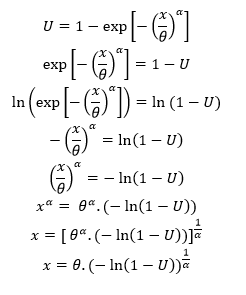
Jadi, hasil transformasi dari distribusi tersebut adalah
![]()
Syntax
| bangkit.weibull=function(n,alpha,teta){
#membuat fungsi untuk membangkitkan n bilangan random yang berdistribusi uniform dengan parameter n, a, dan b(batas interval) U=runif(n,0,1) #dimisalkan U~unif(0,1) x=(teta)*((-log(1-U))^(1/alpha)) #menghitung nilai random yang berdistribusi uniform return(x) #return nilai x sebagai output fungsi } data = bangkit.weibull(100,5,3)#contoh pemanggilan fungsi bangkit.weibull untuk n = 100, alpha = 5, dan tetha = 3 data ks.test(data,’pweibull’,5,3)#uji Kolmogorov-smirnov untuk mengecek apakah berdistribusi weibull atau tidak
|
Output
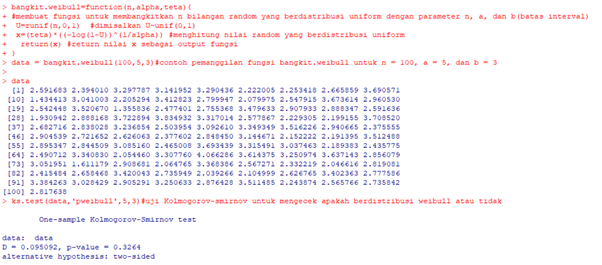
Uji Goodness of Fit
- Hipotesis:
H0= data berdistribusi Weibull dengan parameter alpha=5 dan theta=3
H1= data tidak berdistribusi Weibull dengan parameter alpha=5 dan theta=3
- Tingkat signifikansi
α =0.05
- Statistik Uji
P-value=0.3264
- Daerah kritik
H0 ditolak jika p-value < α =0.05
- Kesimpulan
H0 tidak ditolak karena p-value > α. Maka dapat disimpulkan bahwa data yang dibangkitkan berdistribusi Weibull dengan parameter alpha=5 dan theta=3

