Oleh: Prof. Dr.rer.nat. Dedi Rosadi
Tim Mahasiswa
Ardifya Nandhia Kirana ( 19/442588/PA/19337 )
Cicilia Debie Simangunsong ( 19/442590/PA/19339 )
Danny Theodore Dunrui ( 19/442591/PA/19340 )
Dinda Awanda Ramadhani (19/440077/PA/19066 )
Nurhalim Subha Permata ( 19/442603/PA/19352 )
Penjelasan Metode Maximum Likelihood
Untuk memodelkan suatu model statistika, kita perlu menghitung estimator yang ada pada model untuk menentukan persamaan model statistikanya. Namun, estimator tersebut sangat sulit untuk dihitungan apalagi jika melibatkan beberapa distribusi seperti distribusi Beta dan distribusi Gamma. Maximum Likelihood Estimator adalah salah satu metode untuk menghitung estimator dari suatu distribusi.
Rumus di atas akan pertama akan dimasukkan ke dalam R dengan fungsi expression untuk dicari turunan pertama dan keduanya yang dibutuhkan dalam matrix.
#Memasukkan rumus fungsi distribusi dengan fungsi expression
loglike=expression(log((1/(x*sigma*(sqrt(2*pi))))*exp((-(log(x)-miu)^2)/(2*(sigma^2)))))
#Mencari turunan pertama fungsi terhadap miu
dla=D(loglike,”miu”)
#Mencari turunan kedua fungsi terhadap miu
ddla=D(dla,”miu”)
#Mencari turunan pertama fungsi terhadap sigma
dlb=D(loglike,”sigma”)
#Mencari turunan kedua fungsi terhadap sigma
ddlb=D(dlb,”sigma”)
#Mencari turunan fungsi terhadap miu lalu terhadap sigma
ddlab=D(dla,”sigma”)
Jika syntax di atas dijalankan akan didapatkan hasil turunan sebagai berikut,
Hasil turunan di atas yang kemudian akan kita masukkan ke dalam syntax fungsi jumlahan hasil turunan dalam fungsi MLE Newton-Raphson yang akan dibuat nantinya,
#Fungsi mencari MLE dengan metode Newton-Raphson
#Parameter adalah x (datset) dan miu 0 serta sigma 0 (nilai inisiasi)
mle.newtonraphson<-function(x,miu0,sigma0){
#Fungsi menghitung jumlahan dari hasil turunan pertama dan kedua fungsi log-likelihood
#Berdasarkan hasil dataset x dan miu dan sigma
dla<-function(x,miu,sigma){
return(sum((1/(x * sigma * (sqrt(2 * pi)))) * (exp((-(log(x) – miu)^2)/(2 * (sigma^2))) * (2 * (log(x) – miu)/(2 * (sigma^2))))/((1/(x * sigma * (sqrt(2 * pi)))) * exp((-(log(x) – miu)^2)/(2 * (sigma^2))))))
}
ddla<-function(x,miu,sigma){
return(sum((1/(x * sigma * (sqrt(2 * pi)))) * (exp((-(log(x) – miu)^2)/(2 * (sigma^2))) * (2 * (log(x) – miu)/(2 * (sigma^2))) * (2 * (log(x) – miu)/(2 * (sigma^2))) – exp((-(log(x) – miu)^2)/(2 * (sigma^2))) * (2/(2 * (sigma^2))))/((1/(x * sigma * (sqrt(2 * pi)))) * exp((-(log(x) – miu)^2)/(2 * (sigma^2)))) – (1/(x * sigma * (sqrt(2 * pi)))) * (exp((-(log(x) – miu)^2)/(2 * (sigma^2))) * (2 * (log(x) – miu)/(2 * (sigma^2)))) * ((1/(x * sigma * (sqrt(2 * pi)))) * (exp((-(log(x) – miu)^2)/(2 * (sigma^2))) * (2 * (log(x) – miu)/(2 * (sigma^2)))))/((1/(x * sigma * (sqrt(2 * pi)))) * exp((-(log(x) – miu)^2)/(2 * (sigma^2))))^2))
}
dlb<-function(x,miu,sigma){
return(sum(-(((1/(x * sigma * (sqrt(2 * pi)))) * (exp((-(log(x) – miu)^2)/(2 * (sigma^2))) * ((-(log(x) – miu)^2) * (2 * (2 * sigma))/(2 * (sigma^2))^2)) + x * (sqrt(2 * pi))/(x * sigma * (sqrt(2 * pi)))^2 * exp((-(log(x) – miu)^2)/(2 * (sigma^2))))/((1/(x * sigma * (sqrt(2 * pi)))) * exp((-(log(x) – miu)^2)/(2 * (sigma^2)))))))
}
ddlb<-function(x,miu,sigma){
return(sum(-(((1/(x * sigma * (sqrt(2 * pi)))) * (exp((-(log(x) – miu)^2)/(2 * (sigma^2))) * ((-(log(x) – miu)^2) * (2 * 2)/(2 * (sigma^2))^2 – (-(log(x) – miu)^2) * (2 * (2 * sigma)) * (2 * (2 * (2 * sigma) * (2 * (sigma^2))))/((2 * (sigma^2))^2)^2) – exp((-(log(x) – miu)^2)/(2 * (sigma^2))) * ((-(log(x) – miu)^2) * (2 * (2 * sigma))/(2 * (sigma^2))^2) * ((-(log(x) – miu)^2) * (2 * (2 * sigma))/(2 * (sigma^2))^2)) – x * (sqrt(2 * pi))/(x * sigma * (sqrt(2 * pi)))^2 * (exp((-(log(x) – miu)^2)/(2 * (sigma^2))) * ((-(log(x) – miu)^2) * (2 * (2 * sigma))/(2 *
(sigma^2))^2)) – (x * (sqrt(2 * pi))/(x * sigma * (sqrt(2 * pi)))^2 * (exp((-(log(x) – miu)^2)/(2 * (sigma^2))) * ((-(log(x) – miu)^2) * (2 * (2 * sigma))/(2 * (sigma^2))^2)) + x * (sqrt(2 *
pi)) * (2 * (x * (sqrt(2 * pi)) * (x * sigma * (sqrt(2 * pi)))))/((x * sigma * (sqrt(2 * pi)))^2)^2 * exp((-(log(x) – miu)^2)/(2 * (sigma^2)))))/((1/(x * sigma * (sqrt(2 * pi)))) * exp((-(log(x) – miu)^2)/(2 * (sigma^2)))) + ((1/(x * sigma * (sqrt(2 * pi)))) * (exp((-(log(x) – miu)^2)/(2 * (sigma^2))) * ((-(log(x) – miu)^2) * (2 * (2 * sigma))/(2 * (sigma^2))^2)) + x * (sqrt(2 * pi))/(x * sigma * (sqrt(2 * pi)))^2 * exp((-(log(x) – miu)^2)/(2 * (sigma^2)))) * ((1/(x * sigma * (sqrt(2 * pi)))) * (exp((-(log(x) – miu)^2)/(2 * (sigma^2))) * ((-(log(x) – miu)^2) * (2 * (2 * sigma))/(2 * (sigma^2))^2)) + x * (sqrt(2 * pi))/(x * sigma * (sqrt(2 * pi)))^2 * exp((-(log(x) – miu)^2)/(2 * (sigma^2))))/((1/(x * sigma * (sqrt(2 * pi)))) * exp((-(log(x) – miu)^2)/(2 * (sigma^2))))^2)))
}
ddlab=ddlba<-function(x,miu,sigma){
return(sum(-(((1/(x * sigma * (sqrt(2 * pi)))) * (exp((-(log(x) – miu)^2)/(2 * (sigma^2))) * (2 * (log(x) – miu) * (2 * (2 * sigma))/(2 * (sigma^2))^2) + exp((-(log(x) – miu)^2)/(2 * (sigma^2))) * ((-(log(x) – miu)^2) * (2 * (2 * sigma))/(2 * (sigma^2))^2) * (2 * (log(x) – miu)/(2 * (sigma^2)))) + x * (sqrt(2 * pi))/(x * sigma * (sqrt(2 * pi)))^2 * (exp((-(log(x) – miu)^2)/(2 * (sigma^2))) * (2 * (log(x) – miu)/(2 * (sigma^2)))))/((1/(x * sigma * (sqrt(2 * pi)))) * exp((-(log(x) – miu)^2)/(2 * (sigma^2)))) – (1/(x * sigma * (sqrt(2 * pi)))) * (exp((-(log(x) – miu)^2)/(2 * (sigma^2))) * (2 * (log(x) – miu)/(2 * (sigma^2)))) * ((1/(x * sigma * (sqrt(2 * pi)))) * (exp((-(log(x) – miu)^2)/(2 * (sigma^2))) * ((-(log(x) – miu)^2) * (2 * (2 * sigma))/(2 * (sigma^2))^2)) + x * (sqrt(2 * pi))/(x * sigma * (sqrt(2 * pi)))^2 * exp((-(log(x) – miu)^2)/(2 * (sigma^2))))/((1/(x * sigma * (sqrt(2 * pi)))) * exp((-(log(x) – miu)^2)/(2 * (sigma^2))))^2)))
}
#Melakukan inisiasi untuk beberapa nilai dan rumus yang digunakan pada perulangan
theta=matrix(c(miu0,sigma0),nrow=2)
miu=theta[1,1]
sigma=theta[2,1]
#Untuk mencatat banyak perulangan
iter=1
#Hessian Matrix
hess=matrix(c(ddla(x,miu,sigma),ddlba(x,miu,sigma),ddlab(x,miu,sigma),ddlb(x,miu,sigma)),nrow = 2,ncol = 2)
#Vektor Gradient/Jacobian
grad=matrix(c(dla(x,miu,sigma),dlb(x,miu,sigma)),nrow = 2)
#Menghitung nilai awal estimasi theta
theta.hat=theta-solve(hess)%*%grad
error=abs(theta.hat-theta)
#Melakukan perulangan (iterasi) hingga nilai error lebih kecil dari batas toleransi yang ditetapkan
#While digunakan karena kita tidak tahu jumlah perulangan yang akan dilakukan
#Digunakan any karena error merupakan vektor 2 bilangan yang akan dibandingkan dengan 1 bilangan
while(any(error>0.000001)){
theta=theta.hat
miu=theta[1,1]
sigma=theta[2,1]
hess=matrix(c(ddla(x,miu,sigma),ddlba(x,miu,sigma),ddlab(x,miu,sigma),ddlb(x,miu,sigma)),nrow = 2,ncol = 2)
grad=matrix(c(dla(x,miu,sigma),dlb(x,miu,sigma)),nrow = 2)
theta.hat=theta-solve(hess)%*%grad
error=abs(theta.hat-theta)
iter=iter+1
}
#Jika error sudah lebih kecil dari batas toleransi yang ditetapkan perulangan berhenti
#Output berikut akan dikeluarkan
cat(“Estimasi Miu sebesar :”,round(theta.hat[1,1],4),”\n”)
cat(“Estimasi Sigma sebesar :”,round(theta.hat[2,1],4),”\n”)
cat(“Diperoleh pada iterasi ke-“,iter,”\n”)
}
Setelah didapatkan syntax di atas, akan dijalankan fungsi tersebut. Kemudian, akan diinput dataset berjumlah 112 ke dalam variabel bernama dataset baru kemudian fungsi akan dipanggil sebagai berikut
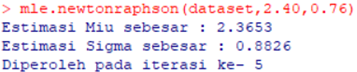
Didapatkan esimasi nilai μ sebesar 2.3653 dan σ sebesar 0.8826 yang didapatkan pada iterasi ke-5. Untuk memastikannya dapat dilihat dengan fungsi fitdistr() dari paket MASS sebagai berikut,
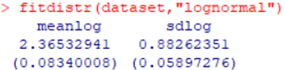
Dapat dilihat bahwa hasil yang didapatkan bahwa dataset yang dimiliki nilai parameter μ sebesar 2.36532941 dan σ sebesar 0.88262351 sama dengan dari fungsi yang dibuat dengan algoritma manual.
Related Posts
Plot Logo Google Drive- Membuat Plot Ucapan Valentine
- Mencari akar fungsi multivariat menggunakan Metode Newton Raphson
- Tutorial: Simulasi monte carlo untuk prediksi penjualan sepatu
- Tutorial: Membangkitkan bilangan random berdistribusi Uniform (a,b) dan berdistribusi Weibul dengan pendekatan metode Inverse Transform